CQUPT-机器学习期末复习

- 大作业

机器学习

1. 归纳等

归纳:从特殊到一般的泛化过程,即从具体的事实归结出一般性的规律

演绎:从一般到特殊的特化过程,从基础原理推演出具体情况.

过拟合:本应该学习样本中的普遍规律,以在面对新样本的时候得到正确的判别.但是学习器的学习太好,导致把训练样本自身的特点当作了样本具有的一般性质,导致泛化能力下降.过拟合无法完全避免.

欠拟合:学习器学习能力地下,不能学习到普遍规律.神经网络可以增加学习轮数,而决策树可以扩展分支来克服.

自助采样:一种划分数据集的方式,用于数据集较小的情况下.它的做法是:

自助采样一般用于数据量较小的情况.

信息熵:信息熵是度量样本集合纯度的指标

数据归一化的原因:数据归一化后,最优解的寻优过程明显会变得更平缓,更容易收敛到最优解.梯度更平缓,梯度下降更快,损失函数收敛更快.

2. 错误率等

错误率:

$$ 错误率 = \frac {错误数} {样本总数} $$

N = 样本总数

精度:

$$ 精度 = 1-错误率 $$

混淆矩阵

预测情况
真实情况正例(Postive)反例(Negative)
正例(Positive)TP(True Positive)FN(False Negative)
反例(Negative)FP(False Positive)TN(True Negative)

第一个 T/F 代表预测是否正确,第二 P/N 代表被预测的结果是 阳性还是阴性

故

查准率:

$$ P = \frac {TP}{TP+FP} $$

查准率代表 预测情况为正例,实际上也为正例所占的比例.

查全率:

$$ R = \frac{TP}{TP+FN} $$

查全率代表 实际情况为正例,被预测为正例所占比利.

不难看出这两者是一个矛盾的量,当一个火灾报警器要确保高查全率,也就是每次火灾要发生了都发出警告,那么不得不对外界因素更加敏感,所以更有可能因为一点点烟而误报,造成的结果就是查准率没那么高.而一个报警器想要提高准确率,那么就必须降低对外界因素的敏感度,于是有可能造成某次真的火灾了并不能报警.这是天然矛盾的.

故我们引入 F1-Score 来评估机器学习模型性能

F1-Score

$$ F1 = \frac {2PR}{P+R} = \frac {2*TP}{样本总数 + TP - TN} $$

测试集:

测试样本组成的集合

训练集:

训练样本组成的集合

留出法:

留出法直接将数据集 D划分为两个互斥的集合，其中一个集合作为训练集S，另一个作为测试集T,在S上训练出模型后，用T 来评估其测试误差，作为对泛化误差的估计.

K 折交叉验证法:

将数据集划分成 K 分,每次取其中 1 份作为测试集,另外K-1份作为训练集,将测试结果取平均值返回.

通常有 5-10-20折交叉验证.

3. P-R 曲线等

P-R 曲线

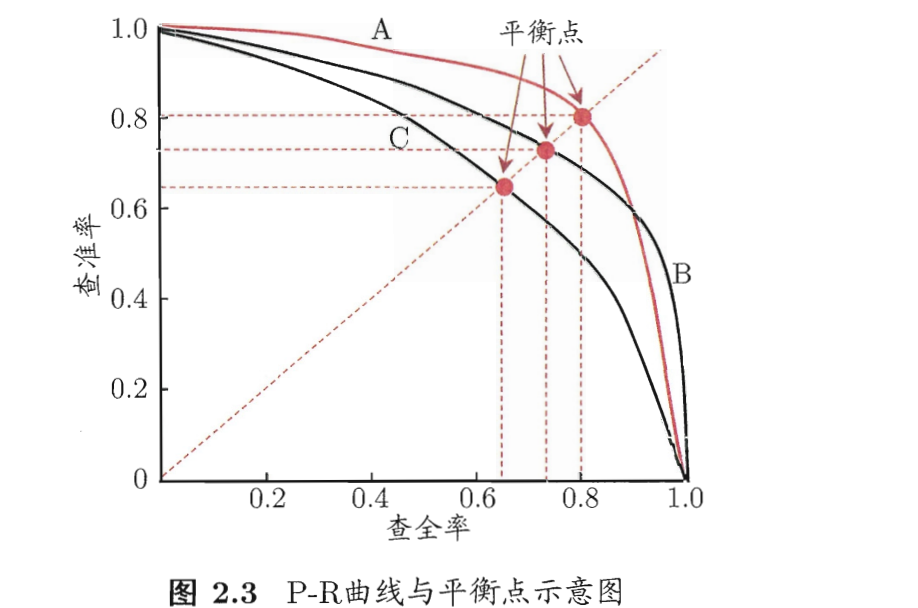
2022-06-23-21-35-20-image.png

平衡点"(Break-Event Point，简称 BEP)是一个综合考虑查准率与查重率的机器学习模型的性能度量，它是"查准率=查全率"时的取值，例如图2.3中学习器C的BEP是0.64，而基于BEP的比较， 可认为学习器A优于B.一般我们使用 F1-score

ROC 曲线

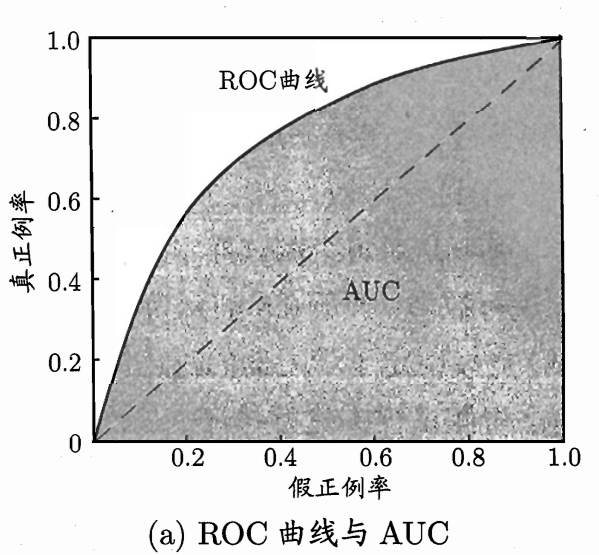
$$ 真正例率= \frac {TP}{TP+FN} $$

$$ 假正例率 = \frac{FP}{FP+FN} $$

AUC : 曲线围成的面积为 AUC 的值! AUC 越大越好.

4. 线性回归等

线性回归:

假设数据有 i 的个属性,那么线性回归试图寻找一组 $\omega$ 来进行预测.

$$ f(x) = \omega_1x_1+\omega_2x_2+…+\omega_ix_i + b $$

其中 $b$ 为截距.线性回归模型可以简写为 $y = \omega^{T}x+b$

分类:

给定一个对象 $x_i$ 将它划分到预定好的某一个类别 $y_i$ 的算法,分类产生的是标记,例如二分类 $y_i \in { 0,1}$

回归:

找数据点之间的联系的分析方法就是回归,回归产生真实的预测值

对数几率回归

线性回归输出的标记是在直线上的变化,那么如果我们的输出标记实际上是在指数尺度上变化,我们该怎么办呢?

我们可以对线性回归的模型进行变化

$$ \ln{z}=\omega^{t}x+b \ z = e^{\omega^{t}+b} $$

这样输出的值就会是指数尺度变化.

更一般的,如果有一个单调可微函数 $g(y)$

那么我们就能得到广义线性模型:

$$ g(z)=\omega^{T}+b \ z = g^{-1}(\omega^{T}+b) $$

其中 g(y) 被称为联系函数.

对数回归 && 对数回归进行分类问题

回归任务给出的值是一个实值,也就是一个数值,但分类问题总会给出一个 $y_i \in {y_0…y_i }$

如果是二分类任务,那么输出的标记 $y \in { 0,1 }$,而回归会给出一个实值,所以我们需要把实际值转化成 0/1

最理想的是"单位阶跃函数",注意这里的 z 实际上是回归模型给出的值.

$$ y = \begin{cases} 0& \text{ if } z<0 \ 0.5& \text{ if } z=0 \ 1& \text{ if } z>0 \end{cases} $$

红色的为阶跃函数!

1.png

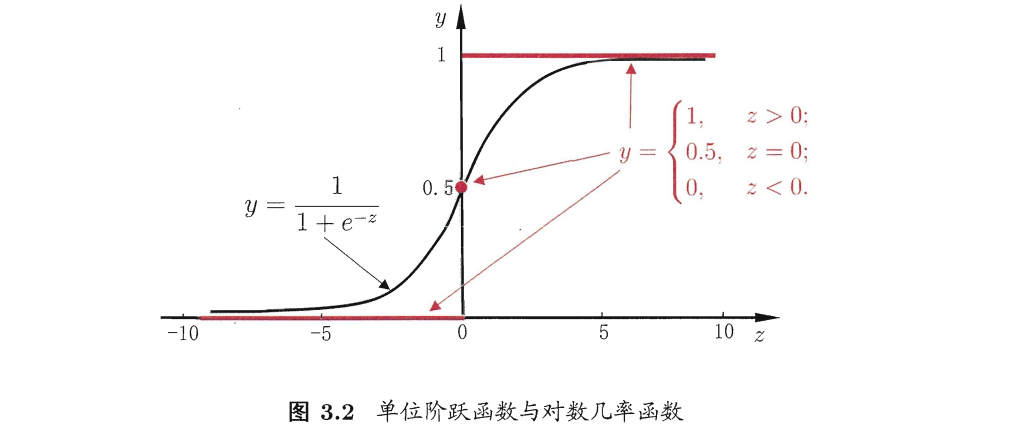
可以看出阶跃函数不连续,不能作为 $g(z)$ 所以我们实际使用的函数是对数几率函数,

如 Sigmoid 函数.

$$ y = \frac {1}{1+e^{-z}} $$

Sigmoid 函数在 0 的附近变化很抖动,并且连续可导,用来做分类非常不错.

$$ 由回归模型给出 \space z = \omega^{T}+b \ 代入到上式 \space y = \frac {1}{1+ e^{ -(\omega^{T}+b)}} $$

那么算出的 $y$ 值就会非常接近0/1/0.5 (0.5 代表可以随便选一个) 也就完成了分类的工作.

对数回归的优点:

  1. 无需假设数据分布

  2. 对率函数会任意阶可导的凸函数,现有的许多数值优化算法可以直接用于求最优解

多分类问题

上面我们讨论了对数几率回归二分类问题,那么接下来我们自然可以想到多分类问题,多分类问题其实也就是把多分类拆成多个二分类.

主要有三个策略:

  1. 一对一 One vs. One –> OvO

  2. 一对其余 One vs. Rest –> OvR

  3. 多对多 Many vs. Many

5. 决策树如何选择分裂点

信息增益法 –ID3决策树[Quinlan,1986]

信息熵:度量样本集合纯度的一种指标.

假定当前样本集合D中第k类样本所占的比例为 $p_k(=1，2……，|Y|)$，则 $D$ 的信息熵定义为:

$$ \begin{align} \tag{4.1} Ent(D) = - \sum_{k=1}^{|Y|} p_k \log_2pk \end{align} $$

$Ent(D)$ 越小 , $D$ 纯度越高. 纯度越高,也就意味这个 D 里面的数据越相似

对于二分类问题,显然 $|Y| == 2 , p_1 = True ,p_2 = False$ .

那么我们到底该怎么利用这个东西进行分类任务呢?

是不是只要划分不断的划分子集,让每个子集的纯度也很高就可以了?

以西瓜书的好瓜,坏瓜为例

好瓜是相似的,坏瓜也是相似的.我们只要按照某些属性进行划分,让每次划分的子集算出来的纯度更高,每次划分都有提升,就可以构造一个树来进行分类了.

怎么算纯度提升?

这里就要引入信息增益了

信息增益定义如下:

$$ \begin{align} \tag{4.2} \begin{split} Gain(D,a) = Ent(D)-\sum_{v=1}^V \frac {|D^v|}{D} Ent(D^v) \end{split} \end{align} $$

假定离散属性 $a$ 有 $V$ 个可能的取值 $ {a^1，a^2，…，a^V}$，若使用 $a$ 来对样本集 $D$ 进行划分，则会产生 $Ⅴ$ 个分支结点，其中第 $v$ 个分支结点包含了 $D$ 中所有在属性 $a$ 上取值为 $a^v$ 的样本，记为 $D^v$ .我们可根据式（4.1）计算出 $D^v$ 的信息熵，再考虑到不同的分支结点所包含的样本数不同，给分支结点赋予权重 $\frac {|D^v|}{|D|}$，即样本数越多的分支结点的影响越大，于是可计算出用属性$a$对样本集 $D$ 进行划分所获得的"信息增益"（information gain）

说白了 $a$ 是所有属性,比如色泽,纹理这样的,根据属性划分,会有 $V$ 个子集 $D^v$.

色泽有 青绿,乌黑,浅白 三个值

那么我们就有 $D^{青绿},D^{乌黑},D^{浅白}$ 三个子集

接着分别计算 每个 $D^N$ 的 $Ent(D^N)$ ,因为每个子集的元素数量不一样,所以你得加权,就是简单的按量加权.

最后求和,用上一次的 $Ent(D)$ 减去和,就能得到按照这个属性分信息增益是多少了

每个属性我都得计算一次,那么信息增益大的,也就说明我按照这个划分得到的子集纯度更高,我就可以按照这个属性进行划分.

不难发现,不管我一开始选择哪个,最后总会遍历完所有的可以选的属性,我第一次是按照色泽分,我分完了之后用纹理分,然后再按其他的,这样树就构造完了.

但是会有这么个情况我按照纹理继续分,结果发现纹理是清晰的全是好瓜,那么我就不用在清晰这个属性下,继续找其他属性划分了,因为这个时候这个$D_n^i$ 纯的不能再纯了,但是纹理是模糊的不够纯,依然有好有坏,我就继续找其他属性分,分到不能再分为止.

这就是按照信息增益来构造决策树的方法,但不代表所有的决策树都按照信息增益分

并且息增益准则对可取值数目较多的属性有所偏好,所以为了减少这个影响,有其他的方法来进行分裂决策树节点.

增益率法 –C4.5 决策树[Quinlan,1993]

这个算法不直接使用信息增益来划分,而是对信息增益进行一定处理

处理如下:

$$ Gain_ratio(D,a) = \frac {Gain(D,a)}{IV(a)} \其中 \ IV(a) = -\sum_{v=1}^{V} \frac{|D^v|}{|D|} \log_2\frac{|D^v|}{|D|} $$

$IV(a)$ 被称为 a 的固有值.

需注意的是，增益率准则对可取值数目较少的属性有所偏好，因此，C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发[Quinlan，1993]:先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的.

基尼指数法 –CART决策树[reiman et al.，1984]

CART 树使用 基尼指数来选择划分属性,数据集 $D$ 的纯度用基尼值来度量:

$$ \begin{equation} \tag{4.5} \begin{split} Gini(D)&={\sum_{k=1}^{|Y|}\sum_{k’\ne k}p_kp_{k’}}\ &= 1-\sum_{k=1}^{|y|}p_k^2 \end{split} \end{equation} $$

观来说，$Gini（D）$ 反映了从数据集$D$中随机抽取两个样本，其类别标记不一致的概率. 因此，$Gini（D）$越小，则数据集D的纯度越高.采用与式（4.2）相同的符号表示，属性 $a$ 的基尼指数定义为

$$ Gini_index(D,a) = \sum_{v=1}^{V}\frac{|D^v|}{|D|}Gini(D^v) $$

选择基尼指数最小的属性作为最有划分属性即可.

6. 感知机缺点等

感知机的缺点:

无法实现 异或门

对于神经网络怎么调节避免 过拟合 与 欠拟合 ,提高准确率

通法:

欠拟合:

  1. 增加数据特征

  2. 使用更高级的的模型

  3. 减少正则化参数

过拟合:

  1. 降低模型复杂度

  2. 数据集扩增

BP神经网络:

过拟合:

  1. 早停:数据分成训练集和验证集,训练集计算梯度,更新连接权,阈值,验证集用来估计误差,如果训练集误差降低而验证集误差升高,停止训练,同时返回具有最小验证集误差的连接权和阈值.

  2. 正则化

深度学习模型为什么需要大量训练样本:

需要更多的数据训练来避免过拟合的发生,以保证训练模型在新的数据上也能有可以接受的表现

神经网络常用的激活函数:

  1. Sigmiod

  2. tanh

  3. Relu

7. SVM 的基本原理

寻找一个区分两类的超平面使得边际最大.

8. 朴素贝叶斯分类器

贝叶斯决策理论方法是统计模型决策中的一个基本方法， 其基本思想是：  1、已知类条件概率密度参数表达式和先验概率。  2、利用贝叶斯公式转换成后验概率。  3、根据后验概率大小进行决策分类。

$$ P(c|x) = \frac {P(c)P(x|c)}{P(x)} $$

其中 $P(c)$ 是类"先验"(prior)概率,$P(x|c)$ 是样本 $x$ 对类标记 $c$ 的类条件概率,或称似然. $P(x)$ 是用于归一化的证据.

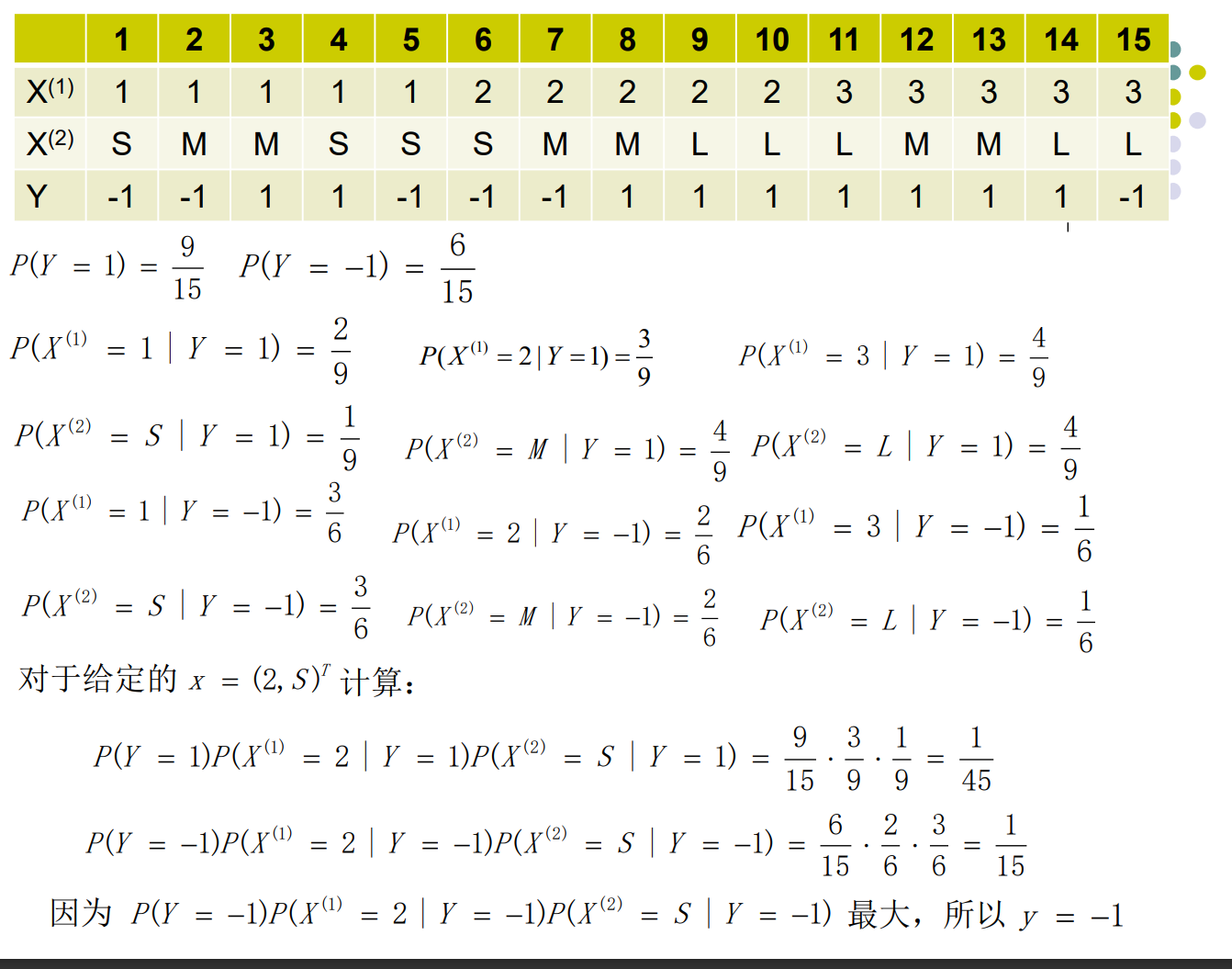
2022-06-24-17-06-59-image.png

在这里:

先验概率: $P(Y = 1 ),P(Y=-1)$ 也就是给定一个数据,这个数据是 $1/0$ 的可能.

条件概率,似然 也就是 $P(X^{(2)}=S \space | \space Y=1)$ 这种,也就是已经是 1 了, $X^{(2)} = S$ 的可能

我们求解的: 后验概率 $P(Y=1|X^{(1)}=S)$,那么反过来就是这个东西已经 $X^{(2)}=S$ 了,那它 $Y=1$的可能是多少.找到最有可能$Y=?$ 也就完成了分类.

什么时候可以用?

特征词独立

9. 集成学习

集成学习：

将一组学习器结合起来。同质集成中个体学习器称为基学习器，相应的算法称为基学习算法。异质集成中的个体学习器由不同的学习算法生成，这时就不会再有基学习算法，相应的个体学习器一般称为组件学习器或个体学习器。集成学习研究的核心是如何生产“好而不同”的学习器

Boosting：

个体学习器之间存在较强依赖关系、必须串行生成的序列化方法。先初始训练一个基学习器，再根据基学习器的表现对训练样本分布进行调整(更多关注分类错误的样本)。Boosting主要关注降低偏差，能够基于泛化能力相当弱的学习器构建出很强的集成。Boosting中，重采样法可以获得"重启动"可以避免因不满足条件而出现的早停，从而持续到预设的T轮。

Bagging：

个体学习器之间不存在强依赖关系、可同时生成的并行化方法。给定一个训练集，对训练集进行采样(可以使用相互交叠的采样子集，通常使用自助采样法，这样就约有63.2%数据在训练集，而剩下的数据可以用于对泛化性能的评估)，产生若干个不同的子集，再从每个子集训练出一个基学习器。Bagging更关注降低方差，因此再不剪枝决策树、神经网络等易受样本扰动的学习器上效果更好。

随机森林：

随机森林是bagging的扩展变体。随机森林的起始性能较差，特别是再集成中只包含一个基学习器，原因是引入了属性扰动，但随着个体学习器数目的增加，随机森林通常能够收敛到更低的泛化误差。随机森林的巽寮效率常优于bagging，bagging使用的是确定型决策树，在选择节点的时候要对节点的所有属性值进行考察；而随机森林使用的是随机型决策树，只需要考察一个属性子集。

同质集成:

集成中只包含同种类型的个体学习器，例如“决策树集成”中全是决策树，“神经网络集成”中全是神经网络，称集成是“同质”的。同质集成中的个体学习器亦称 基学习器(base learner)，相应的学习算法称为 “基学习算法”

异质集成：

集成中的个体学习器由不同的学习算法生成，例如同时包含决策树和神经网络，这样的集成是“异质”的(heterogenous)。

异质集成中个体学习器常称为 组件学习器或直接称为个体学习器。

AdaBoost中AdditiveModel是啥：

考虑加法模型

10. 降维概念以及基础

降维的概念及最基本的方法概念：

通过某种数学变换将原始高维属性空间转换成一个低维"子空间"，在这个子空间中样本密度大幅提高，距离计算也变得更为容易。

为什么能进行降维？

因为在很多时候，人们观测或收集到的数据样本虽然是高维的，但是与学习任务紧密相关的只是某一些低维成分，即高维空间中的一个低维"嵌入"。

聚类的概念

聚类是针对给定的样本，依据它们特征的相似度或距离，将其归并到若干个“类”或“簇”的数据分析问题。其结果满足，类内部相似，类之间不相似

特征选择:

在特征选择中涉及到两个过程,一个是子集搜索,一个是子集评价

11.监督学习和无监督学习

无监督学习:

训练样本的标记信息是未知的,没有 $y_i$ 标签,目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步数据分析提供基础. 这类问题研究最多的是 聚类

有监督学习:

根据已有的数据集,知道输入和输出结果之间的关系.根据这种已知的关系,训练得到一个最优的模型.已知标签 $y_i$ .

12. L1 范数 和 L2 范数的表示,效果

L1 范数:

是什么?

L1 范数是向量中,各个元素的绝对值之和/

有什么用?

让参数矩阵 $\omega$ 稀疏化,可以做特征选择

L2 范数:

是什么?

L2 范数是向量中,各个元素的平方和,然后求平方根

有什么用?

让参数 $\omega$ 的各个值都很小,防止过拟合,提高模型的泛化能力

可以看到L1范数趋向选择少量的特征,其他特征的权重为0,而L2趋向选择更多的特征,但是每个特征的权重都很小